Week 02: Dynamic Programming
Table of contents
Beach Bars
Goal: Find best location for the beach bar by minimizing the maximum distance that any of potential customers within the radius of 100 m must walk.
Input
- We have the total number
nand the coordinates of the parasols, where coordinates are also integers (positive & negative) relative to the origin (the parking lot).
Output
- 1st line with
max_no_of_parasols[space]min_longest_dist - 2nd line with coordinates of all possible optimal locations, sorted from low to high
Optimality of the location x
- A location x on the beach can only have integer coordinates and is optimal if the number of parasols within 100m of it (i.e. with coordinates in
[x − 100, x + 100]) is maximal with respect to all other locations on the beach.- If many locations maximize the number of parasols we only want those such that the distance to the farthest parasol at most 100m away is minimized.
Solution Technique
The parasols each associates with an int value as its coordinate on a 1D line, and therefore it appears natural to have the container that contains the coordinates sorted.
The optimality of the solution is determined by the following two criteria:
- Number of parasols within the range (to be maximized)
max_num - Minimum distance to the furthest parasol (to be minimized)
min_dist- the min distance would be the center
To find the optimal solution, we need to find a way to iterate over the parasol coordinates while keeping track of the above criteria and update values accordingly. Having criteria also implicitly implies that we shall have case distinctions for updating max_num and min_dist, when comparing them against the values computed from the current iteration.
Sliding Window (SW)
The problem setup includes a fixed size window of size 200 meters, which is suitable for using the SW technique.
We use two pointers left and right, each represent an index to access a parasol coordinate in the container. We use it for keeping track of the parasols that fit into the fixed-size window in the current iteration.
Edge Case: Parity
To find the center within an interval, we can simply divide the interval by two. However, we are considering int coordinates, and for odd intervals, we need to take two centers that are equally good for the 2nd criterion into account.
We perform a division check using the standard std::div function, and fetch the remainder div_res.rem and the quotient div_res.quot from the div_res object.
Burning Coins
Input
We have total number of n coins, each associated with a positive integer value \(1 \leq v_{i} \leq 2500\)
Output
single line of largest winning max_win
Problem Modeling
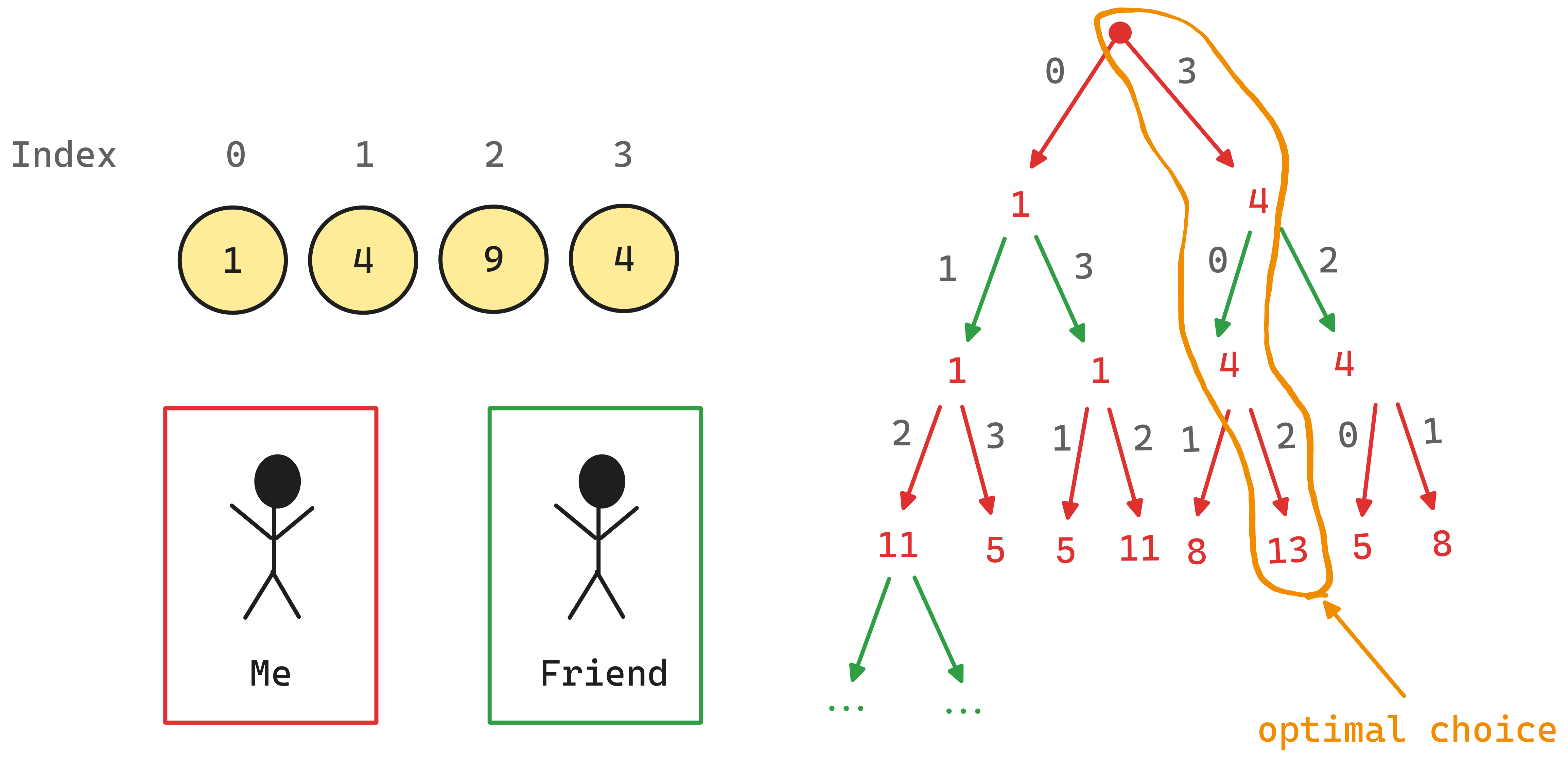
Solution Technique
In this exercise we shall not sort and coins but need to preserve its original ordering.
The overall technique boils down to recursive calls with memoization and with a time complexity of \(O(n^{2})\).
LeetCode 877. Stone Game is a very similar exercise that inspired this solution technique. See this YouTube video to see how this problem is tackled.
Defensive Line
Input
Output
LeetCode 698. Partition to K Equal Sum Subsets (Medium) and LeetCode 689. Maximum Sum of 3 Non-Overlapping Subarrays (Hard).