ACT4E Python library |

Solving real-life problems

by recognizing the algebraic structures for a familiar engineering domain, one can utilize these compositionality structures to achieve either more elegance or efficiency

Application: Currency optimization problem

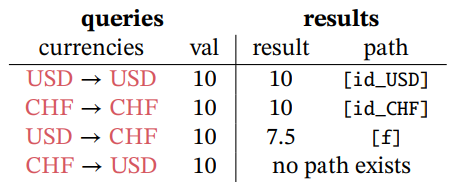
set-up of the problem

In this set-up we were asked to implement an algorithm which outputs the optimal path from the source currency to the target currency such that the resulting amount of money after the currency exchange is maximized.

In our approach, we define the currency category Curr which enables us to model currencies as objects of a category, and morphisms will describe exchanging between those currencies.

We can formally define this category as followed:

formal definition

After recognizing the algebraic structure in this modelling problem, the rest of the implementation is then trivial by utilizing the implemented Python library. The implementation for semicategory_concrete.py is illustrated below.

from typing import TypedDict, Any, TypeVar, List
import act4e_interfaces as I
import networkx as nx
import math
from numpy import identity
from act4e_solutions.semicat_repr_helper import ToolSet, EQ

# TypeVar
MD = TypeVar("MD")

class CurrencyOptimization(I.CurrencyOptimization):
    def compute_optimal_conversion(self,
                                   available: I.SemiCategory[I.RichObject[str],
                                   I.RichMorphism[I.CurrencyExchanger]],
                                   source: str,
                                   amount: float,
                                   target: str) -> I.OptimalSolution:
        
        final_amount: float


        # STEP 1: return all morphisms from 'source' to 'target'
        # def hom(self, ob1: Ob, ob2: Ob, uptolevel: Optional[int] = None) -> I.EnumerableSet[Mor]:
        rich_obj1 = I.RichObject(source, source)
        rich_obj2 = I.RichObject(target, target)

        homset_src_dst = available.hom(rich_obj1, rich_obj2, uptolevel=1)
        hom_elements = list(homset_src_dst.elements())

        path_labels = ""
        final_amount = 0.

        for mor in hom_elements:
            outcome = self.exchanged(amount, mor.mordata)
            if outcome > final_amount:
                path_labels = mor.label
                final_amount = outcome
        return I.OptimalSolution([path_labels], final_amount)


    def exchanged(self, x: float, curr: I.CurrencyExchanger)-> float:
        """Given a CurrencyExchanger
           Returns the exchanged value
        """
        fx = x * curr.rate - curr.commission
        return fx

Visualization of some algebraic structures

For sake of the simplicity, we integrated the networkx library for solving certain problems. We then added a graphical representation layer which gives us a simple-to-use interface for visualizing many algebraic structures.

solving poset closure problem

ACT4E Python library

Solving real-life problems

Application: Currency optimization problem

Visualization of some algebraic structures

References

2022